マイコン宇宙講座-惑星探査機の軌道追跡
最近、小惑星リュウグウにサンプル・リターンして、持ち帰ったサンプルからアミノ酸を始めとする25種類のサンプルが発見されたことは有名なニュースです。その前は、小惑星イトカワにサンプル・リターンに挑戦し、満身創痍になりながらも地球へ帰還し、サンプルを持ち帰りました。映画になるほど有名になりましたね。
探査機の打ち上げは月に始まります。ソ連と米国の宇宙開発競争ですね。月に人類を到達させたのは米国でアポロ11号です。アポロ計画は1972年アポロ17号を最後に、それ以降は月へ人類を送っていません。さて、月以外はどうでしょう。金星、火星、木星、土星、天王星、海王星とさまざまな惑星へ探査機を送っています。このうち、地表へ到達できるのは金星と火星のみで、それ以外は軌道上からの撮影です。それでも、鮮明な写真により地球からわからないことがたくさん発見されました。
サブルーチン ecliptic_coordinates_xyz
※サブルーチンはlib.pyに記述してください。
# KOUDO ZAHYO from XYZ
def ecliptic_coordinates_xyz(x, p, K):
xe = x[1][p]
ye = x[2][p] * K[4] + x[3][p] * K[5]
ze = -x[2][p] * K[5] + x[3][p] * K[4]
ss = ye
cc = xe
tt = quadrant(ss, cc)
lp = tt
cc = ye / math.sin(lp)
ss = ze
bp = math.atan(ss / cc)
r0 = math.sqrt(xe * xe + ye * ye + ze * ze)
return lp, bp, r0サブルーチン print_elements_display
※サブルーチンはlib.pyに記述してください。
def print_elements_display(td, pe, ec, nd, ic, no, q, K, T):
jd = td
yy, mm, dd = jdate(jd, T)
a = q / (1.0 - ec)
pd = pow(a, 1.5)
print(' T = %4d %2d %6.3f ET' % (yy, mm, dd))
print(' Peri.= %7.3f e = %9.5f' % (pe * K[3], ec))
print(' Node = %7.3f (1950) a = %9.5f' % (nd * K[3], a))
print(' Inc. = %7.3f n = %9.6f' % (ic * K[3], no * K[3]))
print(' q = %8.5f (AU) P = %4.2f 年' % (q, pd))
return aメインルーチン m49.py
このプログラムでは、探査機の軌道が楕円軌道を描いたときのみとされています(「マイコン宇宙講座」115頁)。ですので、計算できない探査機もあります。
# m49.py
# マイコン宇宙講座
# 4-9 惑星探査機の軌道追跡プログラム
from PIL import Image, ImageDraw, ImageFont
from tkinter.constants import SOLID
import tkinter as tk
import math
import lib
def drawing_frame(jd, from_planet, to_planet, frame_color, sun_color, fonts, draw):
draw.rectangle((1, 1, 640, 400), outline=frame_color, width=1)
draw.line((96, 1, 96, 400), fill=frame_color, width=1)
draw.line((536, 1, 536, 400), fill=frame_color, width=1)
draw.line((536, 96, 640, 96), fill=frame_color, width=1)
draw.line((536, 224, 640, 224), fill=frame_color, width=1)
draw.line((536, 304, 640, 304), fill=frame_color, width=1)
draw.ellipse((316, 196, 324, 204), fill=sun_color)
for ln in range(326, 520, 5):
draw.line((ln, 200, ln + 2, 200))
draw.line((520, 200, 515, 195))
draw.line((520, 200, 515, 205))
yy, mm, dd = lib.jdate(jd, lib.T)
draw.text((544, 16), ' 打ち上げ日', font=fonts)
draw.text((544, 48), ' %4d 年' % (yy), font=fonts)
draw.text((544, 64), ' %02d 月 %02d日' % (mm, dd), font=fonts)
draw.text((544, 128), 'From', font=fonts)
draw.text((544, 144), ' ' + from_planet, font=fonts)
draw.text((544, 176), 'To', font=fonts)
draw.text((544, 192), ' ' + to_planet, font=fonts)
draw.text((542, 240), '探査機の速度', font=fonts)
draw.text((540, 272), ' %4.1f Km/Sec' % (vo1), font=fonts)
draw.text((544, 320), ' 飛行速度', font=fonts)
draw.text((4, 16), ' 到着日', font=fonts)
# メイン
x = [[0 for i in range(10)] for j in range(4)]
f = [0, 0, 0, 0]
q = [0, 0, 0, 0]
ww = [0, 0, 0]
jd = [0, 0, 0]
pln = [0, 0, 0]
lp = [0, 0, 0]
bp = [0, 0, 0]
r = [0, 0, 0]
r0 = [0, 40, 40, 40, 25, 8, 4]
print('\n')
pln[1] = input('打ち上げ惑星の番号 ? ')
pln[1] = int(pln[1])
std = input('打ち上げ日と時刻 ? ')
dy, dt = std.split(',')
dy = float(dy)
dt = float(dt)
jde, yy, mm, dd, hh, ms, ss = lib.mjd(dy, dt)
jd[1] = jde
pln[2] = input('目的惑星の番号 ? ')
pln[2] = int(pln[2])
std = input('到着日と時刻 ? ')
dy, dt = std.split(',')
dy = float(dy)
dt = float(dt)
jde, yy, mm, dd, hh, ms, ss = lib.mjd(dy, dt)
jd[2] = jde
print('\n')
# 打ち上げ惑星
t1 = jd[1] - 33281.92334
t1 = t1 * (2.737909288e-5 + 1.260132857e-17 * t1)
t2 = t1 * t1
e, m, p, n, i, a, rd = lib.mean_elements(pln[1], t1, t2)
pe = p
nd = n
ic = i
ax1 = a
f, q = lib.eph_const(pe, nd, ic, lib.K)
ec = e
mo = m / (2.0 * math.pi)
mo = 2.0 * math.pi * (mo - int(mo))
ss, cc, ff = lib.kepler(mo, ec)
b = a * math.sqrt(1.0 - e * e)
for n in range(1, 4):
f[n] = a * f[n]
q[n] = b * q[n]
for n in range(1, 4):
x[n][pln[1]] = ff * f[n] + ss * q[n]
lp[1], bp[1], r[1] = lib.ecliptic_coordinates_xyz(x, pln[1], lib.K)
# 目的惑星
t1 = jd[2] - 33281.92334
t1 = t1 * (2.737909288e-5 + 1.260132857e-17 * t1)
t2 = t1 * t1
e, m, p, n, i, a, rd = lib.mean_elements(pln[2], t1, t2)
pe = p
nd = n
ic = i
ax2 = a
f, q = lib.eph_const(pe, nd, ic, lib.K)
ec = e
mo = m / (2.0 * math.pi)
mo = 2.0 * math.pi * (mo - int(mo))
ss, cc, ff = lib.kepler(mo, ec)
b = a * math.sqrt(1.0 - e * e)
for n in range(1, 4):
f[n] = a * f[n]
q[n] = b * q[n]
for n in range(1, 4):
x[n][pln[2]] = ff * f[n] + ss * q[n]
lp[2], bp[2], r[2] = lib.ecliptic_coordinates_xyz(x, pln[2], lib.K)
if lp[2] < lp[1]:
lp[2] = lp[2] + 2.0 * math.pi
cc = math.cos(bp[2]) * math.sin(lp[2] - lp[1])
ss = math.cos(bp[1]) * math.sin(bp[2]) - math.sin(bp[1]) * math.cos(bp[2]) * math.cos(lp[2] - lp[1])
ic = math.atan(ss / cc)
ss = ss / math.sin(ic)
cc = math.sin(bp[1]) * math.sin(bp[2]) + math.cos(bp[1]) * math.cos(bp[2]) * math.cos(lp[2] - lp[1])
tt = lib.quadrant(ss, cc)
u2 = tt
if ic < 0:
nd = lp[1] - math.pi
if nd < 0:
nd = nd + 2.0 * math.pi
if ic > 0:
nd = lp[1]
bb = 0.1
i = 1
ps = 0.1
ps1 = ps
# goto 555
while True:
ps = ps
q1 = ps / r[1] - 1.0
q2 = ps / r[2] - 1.0
cc = q1
ss = (q1 * math.cos(u2) - q2) / math.sin(u2)
tt = lib.quadrant(ss, cc)
v1 = tt
v2 = v1 + u2
ec = math.sqrt(ss * ss + cc * cc)
if ec > 0.99:
ps = ps + 0.05
ps1 = ps
continue
a = ps / (1.0 - ec * ec)
no = lib.K[1] / pow(a, 1.5)
e1 = 2.0 * math.atan(math.sqrt((1.0 - ec) / (1.0 + ec)) * math.tan(v1 / 2.0))
e2 = 2.0 * math.atan(math.sqrt((1.0 - ec) / (1.0 + ec)) * math.tan(v2 / 2.0))
m1 = e1 - ec * math.sin(e1)
m2 = e2 - ec * math.sin(e2)
if m1 > m2:
m2 = m2 + 2.0 * math.pi
tc = (m2 - m1) / no
ww[i] = tc - (jd[2] - jd[1])
print(' PS=%8.5f BB=%9.5f WW=%10.2f e=%7.4f' % (ps, bb, ww[i], ec))
if abs(ww[i]) < 0.5:
break
if i != 2:
i = 2
ps1 = ps
ps = ps + bb
continue
if ww[1] * ww[2] >= 0:
i = 2
ps1 = ps
ps = ps + bb
ww[1] = ww[2]
continue
print('-----------------------------------------------------')
ps = ps1
i = 1
bb = bb / 10.0
print('NEW PS=%9.5f\n' % (ps))
# 近似パス 軌道要素の計算
pe = -v1
if ic < 0:
pe = math.pi - v1
if pe < 0:
pe = pe + 2.0 * math.pi
if pe > 2.0 * math.pi:
pe = pe - 2.0 * math.pi
ic = abs(ic)
q = a * (1 - ec)
td = jd[1] - m1 / no
print('\n\n 惑星探査機の軌道\n')
print(' from ' + lib.PL[pln[1]] + ' to ' + lib.PL[pln[2]] + '\n')
a = lib.print_elements_display(td, pe, ec, nd, ic, no, q, lib.K, lib.T)
vo1 = 29.785 * math.sqrt(2.0 / r[1] - 1 / a)
vo2 = 29.785 * math.sqrt(2.0 / r[1] - 1 / ax1)
print('\n 打ち上げ速度 = %8.3f Km/Sec' % (vo1 - vo2))
print(' 探査機の速度 = %8.3f Km/Sec' % (vo1))
print(' 地球の速度 = %8.3f Km/Sec' % (vo2))
print('\n')
# std = input('PRESS ANY KEY ')
root = tk.Tk()
root.resizable(False, False)
root.geometry('644x440')
root.title('マイコン宇宙講座 - 惑星探査機の軌道追跡プログラム')
img = Image.new('RGB', (642, 402), (0, 0, 0))
draw = ImageDraw.Draw(img)
canvas = tk.Canvas(root, width=642, height=402, bg='black')
canvas.pack(anchor=tk.NW)
# フォント名は実行環境に合わせて変更すること
fonts = ImageFont.truetype('ipag.ttf', 15)
# カラーパレット
frame_color = (255, 255, 255)
sun_color = (255, 0, 0)
orbit_color = (0, 20, 175)
# フレーム描画
from_planet = lib.PL[pln[1]]
to_planet = lib.PL[pln[2]]
drawing_frame(jd[1], from_planet, to_planet, frame_color, sun_color, fonts, draw)
ro = r0[pln[2]]
i1 = int(jd[2] - jd[1])
i2 = i1 / 15
iv = int(i2)
jde = jd[1]
while True:
t1 = jde - 33281.92334
t1 = t1 * (2.737909288e-5 + 1.260132857e-17 * t1)
t2 = t1 * t1
yy, mm, dd = lib.jdate(jde, lib.T)
draw.rectangle((4, 16, 94, 96), fill=(0, 0, 0))
draw.text((4, 16), ' 到着日', font=fonts)
draw.text((8, 48), ' %4d 年' % (yy), font=fonts)
draw.text((8, 64), '%02d 月 %02d 日' % (mm, dd + 0.375), font=fonts)
for cnt in range(1, 3):
pn = pln[cnt]
e, m, p, n, i, ap, rd = lib.mean_elements(pn, t1, t2)
mo = m / (2.0 * math.pi)
mo = 2.0 * math.pi * (mo - int(mo))
ss, cc, ff = lib.kepler(mo, e)
b = ap * math.sqrt(1.0 - e * e)
ss = b * ss
cc = ap * ff
tt = lib.quadrant(ss, cc)
v = tt
pp = n + p
vv = v + pp
rr = ro * math.sqrt(ss * ss + cc * cc)
x = rr * math.cos(vv)
y = rr * math.sin(vv)
y = -y
x = int(x + 80)
y = int(y + 50)
if int(jde) != int(jd[1]):
x = x * 4
y = y * 4
draw.rectangle((x - 1, y - 1, x + 1, y + 1), fill=(255, 255, 255))
# continue
if pln[2] <= 3:
if x >= 80:
x = (x + 6) * 4
y = (y + 6) * 4
draw.text((x, y), lib.PL[pln[cnt]], font=fonts)
elif x < 80:
x = (x - 6) * 4
y = (y - 6) * 4
draw.text((x, y), lib.PL[pln[cnt]], font=fonts)
if pln[cnt] != 3:
if x < 80:
if y > 50:
x = (x - 7) * 4
y = (y - 10) * 4
draw.text((x, y), lib.PL[pln[cnt]], font=fonts)
else:
x = (x + 8) * 4
y = y * 4
draw.text((x, y), lib.PL[pln[cnt]], font=fonts)
else:
if y > 50:
x = (x - 18) * 4
y = y * 4
draw.text((x, y), lib.PL[pln[cnt]], font=fonts)
else:
x = x * 4
y = (y + 10) * 4
draw.text((x, y), lib.PL[pln[cnt]], font=fonts)
elif x < 80:
x = (x - 18) * 4
y = y * 4
draw.text((x, y), lib.PL[pln[cnt]], font=fonts)
else:
x = (x + 8) * 4
y = y * 4
draw.text((x, y), lib.PL[pln[cnt]], font=fonts)
draw.rectangle((x - 1, y - 1, x + 1, y + 1), fill=(255, 255, 255))
# 探査機のプロット
mo = no * (jde - td)
ss, cc, ff = lib.kepler(mo, ec)
b = a * math.sqrt(1.0 - ec * ec)
ss = b * ss
cc = a * ff
tt = lib.quadrant(ss, cc)
v = tt
rs = math.sqrt(ss * ss + cc * cc)
pp = nd + pe
vv = v + pp
rr = ro * rs
x = rr * math.cos(vv)
y = rr * math.sin(vv)
y = -y
x = int(x + 80) * 4
y = int(y + 50) * 4
draw.rectangle((x - 1, y - 1, x + 1, y + 1))
vo1 = 29.785 * math.sqrt(2.0 / rs - 1 / a)
draw.rectangle((540, 352, 638, 370), fill=(0, 0, 0))
draw.text((540, 352), ' %4.1f Km/Sec' % (vo1), font=fonts)
if abs(jde - jd[2]) <= iv:
draw.rectangle((30, 104, 64, 360), outline=frame_color, width=1)
draw.text((40, 112), '惑', font=fonts)
draw.text((40, 144), '星', font=fonts)
draw.text((40, 176), '探', font=fonts)
draw.text((40, 208), '査', font=fonts)
draw.text((40, 240), '機', font=fonts)
draw.text((40, 272), 'の', font=fonts)
draw.text((40, 304), '軌', font=fonts)
draw.text((40, 336), '道', font=fonts)
if jde < jd[2] + iv:
jde = jde + iv
continue
else:
break
draw.text((4, 368), ' END', font=fonts)
# 描画した星座の画像を保存
img.save('./images/course.png')
# プロット結果の表示
photo = tk.PhotoImage(file='./images/course.png')
canvas.create_image(1, 1, image=photo, anchor=tk.NW)
button = tk.Button(root, text='閉じる', width=6, relief=SOLID, cursor='hand1', command=root.destroy)
button.place(x=558, y=407)
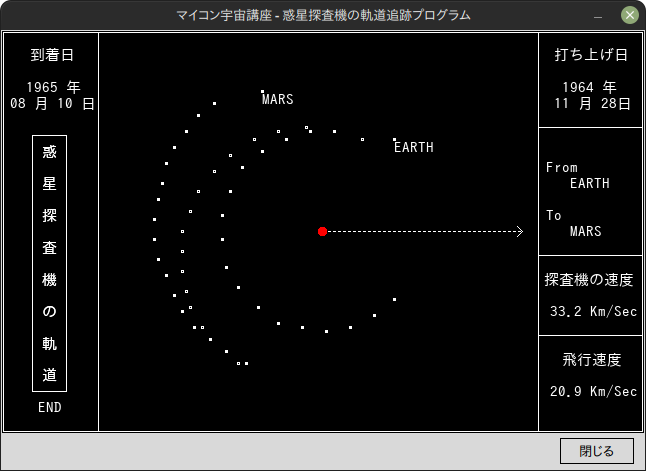
root.mainloop()例題 マリーナ4号は、1964年11月28日に1965年7月14日から15日に火星へ接近しました。打ち上げから火星までの軌道を描いてみよう。なお、時刻は9時とします。
打ち上げ惑星の番号 ? 3
打ち上げ日と時刻 ? 19641128,090000
目的惑星の番号 ? 4
到着日と時刻 ? 19650715,090000
PS= 1.05000 BB= 0.10000 WW= 2401.94 e= 0.8526
PS= 1.15000 BB= 0.10000 WW= 133.10 e= 0.3703
PS= 1.25000 BB= 0.10000 WW= -44.90 e= 0.3266
-----------------------------------------------------
NEW PS= 1.15000
PS= 1.15000 BB= 0.01000 WW= 133.10 e= 0.3703
PS= 1.16000 BB= 0.01000 WW= 101.55 e= 0.3300
PS= 1.17000 BB= 0.01000 WW= 74.91 e= 0.2938
PS= 1.18000 BB= 0.01000 WW= 52.15 e= 0.2632
PS= 1.19000 BB= 0.01000 WW= 32.51 e= 0.2405
PS= 1.20000 BB= 0.01000 WW= 15.40 e= 0.2280
PS= 1.21000 BB= 0.01000 WW= 0.37 e= 0.2275
惑星探査機の軌道
from EARTH to MARS
T = 1964 11 23.539 ET
Peri.= 355.025 e = 0.22746
Node = 65.593 (1950) a = 1.27602
Inc. = 0.158 n = 0.683783
q = 0.98578 (AU) P = 1.44 年
打ち上げ速度 = 3.026 Km/Sec
探査機の速度 = 33.217 Km/Sec
地球の速度 = 30.191 Km/Sec