マイコン宇宙講座-日食シミュレーション
天文現象のひとつである日食は、その昔、不吉な天変地異として恐れられていました。太陽神として崇められていた太陽が黒くなるなどということはあってはならないことだったからです。現在は素晴らしい天文現象であり、めったに見ることができない太陽の姿を見ることができます。
日食は、ご存知のように太陽が月によって隠される現象です。太陽をどれだけ隠すかを食分といい、数値で表すことができます。食分1.0は、月が太陽を完全に隠すことを意味しています。これを皆既日食といいます。皆既日食は、地球から月までの距離によって、月の大きさが見かけ上変わるため、いろいろな現象を見せてくれます。月の見かけ上の大きさが太陽より小さい場合は、金環食と呼ばれ、月が移動していくことによって、ダイアモンドリングやベイリー・ビーズといった現象をみることができます。
今後、日本で見ることのできる日食は、2023年4月20日の金環皆既日食ですが、日本からだ九州南部以南で食分の小さい部分日食としてみることができるようです。それ以降2030年まで起きる日食は見ることはできません。なかなか貴重な天文現象です。
メインルーチン m511.py
入力する計算間隔の値をあまり小さくしないでください。計算した値を最大40までストックできますが、小さくすると作成される画像の枚数も併せて増えてししまい、日食を最後まで表示することができなくなります。ですので計算間隔は最小5分までとしてください。変数max_countの値を変更することで回避できますが、消費するメモリ量が増えてしまいます。GIFアニメーションを作成する以外はデフォルトの設定で実行してください。
# my511.py
# マイコン宇宙講座
# 5-11 日食シミュレーションプログラム
#
# 要インストール
# sudo apt install python3-pil.imagetk
from PIL import Image, ImageDraw, ImageFont
from tkinter.constants import SOLID
import tkinter as tk
import glob
import os
import math
import lib
M2PI = 2.0 * math.pi
# 観測地
# lg = 139.745 / lib.K[3]
# la = 35.654 / lib.K[3]
# obs = '東京 '
#
# lg = 141.682 / lib.K[3]
# la = 45.419 / lib.K[3]
# obs = '稚内 '
#
# lg = 141.350 / lib.K[3]
# la = 43.050 / lib.K[3]
# obs = '札幌 '
#
# lg = 138.180 / lib.K[3]
# la = 36.630 / lib.K[3]
# obs = '長野 '
#
lg = 124.1392 / lib.K[3]
la = 24.3731 / lib.K[3]
obs = '石垣島天文台 '
max_count = 40
ds = [0, 0, 0]
year = [0 for i in range(max_count)]
month = [0 for i in range(max_count)]
day = [0 for i in range(max_count)]
hour = [0 for i in range(max_count)]
minute = [0 for i in range(max_count)]
xpos = [0 for i in range(max_count)]
ypos = [0 for i in range(max_count)]
sun_radius = [0 for i in range(max_count)] # RR
moon_radius = [0 for i in range(max_count)] # LL
print()
std = input('DATE AND TIME(JST) ? ')
dy, dt = std.split(',')
dy = float(dy)
dt = float(dt)
jd, yy, mm, dd, hh, ms, ss = lib.mjd(dy, dt)
iv = input('INTERVAL(UNIT OF MINUTE) ? ')
iv = float(iv)
# eclipseフォルダにファイルがある場合は削除
for files in glob.glob('./images/eclipse/*.png'):
os.remove(files)
i = 0
ii = 0
yz = 0
mz = 0
print()
print(' %-8s ( JST ) 月の座標 太陽と月の大きさ 食分' % (obs))
print(' ---------------------------------------------------------------------------------')
print(' 年 月 日 時 分 - X - - Y - 。 。 ,')
while True:
ta = (jd - 15019.5) / 36525.0
a, b, c, d, e, g, j, l, m, n, v, w = lib.argument(ta)
mx, my, mz = lib.moon(ta, a, b, d, e, n, g, w)
r0 = c
r1 = mx
r2 = my
r3 = mz
ra, dc, dl = lib.positions(r0, r1, r2, r3)
ds[1] = dl
if ra < 0:
ra = ra + M2PI
r1 = la
r2 = lib.geocentric_distance(r1) # 地心距離
r0 = r2 / 6378.16
r1 = la
r2 = 0
r3 = lib.geocentric_latitude(r1, r2) # 地心緯度
fi = r3
r1 = jd
r2 = lg
r3 = lib.siderealtime_date(r1, r2) # 平均春分点に準拠した地方恒星時
s1 = r3
x0 = r0 * math.cos(fi) * math.cos(s1)
y0 = r0 * math.cos(fi) * math.sin(s1)
z0 = r0 * math.sin(fi)
xx = dl * math.cos(dc) * math.cos(ra)
yy = dl * math.cos(dc) * math.sin(ra)
zz = dl * math.sin(dc)
x = xx - x0
y = yy - y0
z = zz - z0
ds[2] = math.sqrt(x * x + y * y + z * z)
ss = y
cc = x
tt = lib.quadrant(ss, cc)
mr = tt
md = math.atan(z / (y / math.sin(mr)))
# SUN R.A AND DECL.
sx, sy, sz = lib.sun(ta, c, g, j, l, m, n, v)
r0 = l
r1 = sx
r2 = sy
r3 = sz
ra, dc, dl = lib.positions(r0, r1, r2, r3)
ds[1] = dl
if ra > M2PI:
ra = ra - M2PI
if ra < 0:
ra = ra + M2PI
x = -(mr - ra) * lib.K[3] * 60.0
y = (md - dc) * lib.K[3] * 60.0
au = ds[1] * 149597870.0
dl = ds[2] * 6378.16
rr = math.atan(695989.0 / au) * lib.K[3] * 60.0
ll = math.atan(1738.68 / dl) * lib.K[3] * 60.0
# MJD TO YY-MM-DD
jd = jd + 0.375
yy, mm, dd = lib.jdate(jd, lib.T)
jd = jd - 0.375
hh = 24.0 * (dd - int(dd))
dd = int(dd)
ms = 60.0 * (hh - int(hh)) + 0.1
hh = int(hh)
if int(ms + 0.1) == 60:
hh = hh + 1
ms = 0
if x ** 2 + y ** 2 > 1250.0 and ii == 0:
jd = jd + iv / 1440.0
continue
if x ** 2 + y ** 2 <= 1250.0:
while True:
year[i] = yy
month[i] = mm
day[i] = dd
hour[i] = hh
minute[i] = ms
xpos[i] = x
ypos[i] = y
sun_radius[i] = rr
moon_radius[i] = ll
i = i + 1
break
sb = (rr + ll - math.sqrt(x * x + y * y)) / (2.0 * rr)
sfmt = ' %2d %2d %2d %6.1f %6.1f %5.1f %5.1f %5.2f' % (dd, hh, ms, x, y, rr, ll, sb)
if yy != yz:
sfmt = ' %4d %2d %2d %2d %2d %6.1f %6.1f %5.1f %5.1f %5.2f' % (yy, mm, dd, hh, ms, x, y, rr, ll, sb)
else:
if mm != mz:
sfmt = ' %2d %2d %2d %2d %6.1f %6.1f %5.1f %5.1f %5.2f' % (mm, dd, hh, ms, x, y, rr, ll, sb)
print(sfmt)
yz = yy
mz = mm
ii = ii + 1
if ii < max_count:
jd = jd + iv / 1440.0
continue
break
print('---------------------------------------------------------------------------------')
print()
std = input('PRESS ANY KEY ')
# 最初のの画像を表示
def display_eclipse():
global count, files
drawing_image_file(files[count])
# ひとつ前の画像を表示
def display_eclipse_prev():
global count, files
count -= 1
if count < 0:
count = 0
drawing_image_file(files[count])
# 次の画像を表示
def display_eclipse_next():
global count, file_number, files
count += 1
if count > file_number - 1:
count = file_number - 1
drawing_image_file(files[count])
def drawing_image_file(picture):
global photo
# 画像の表示
photo = tk.PhotoImage(file=picture)
canvas.create_image(1, 1, image=photo, anchor=tk.NW)
# 画像の最上部にファイル番号を描く
def drawing_file_number(fn, draw, fonts):
s = str(fn)
sfn = s.zfill(5)
draw.rectangle((550, 5, 638, 15), fill=(0, 0, 0))
draw.text((550, 5), 'No.: ' + sfn, font=fonts)
# 日食を描く
def drawing_sun_eclipse():
global year, month, day, hour, minute, xpos, ypos, sun_radius, moon_radius
img = Image.new('RGB', (640, 400), (0, 0, 0))
draw = ImageDraw.Draw(img)
# 太陽と月のカラーパレット
moon_color = (15, 15, 20)
sun_color = (255, 255, 255)
# フォント名は実行環境に合わせて変更すること
# TrueTypeの等幅フォント名を指定する
fonts = ImageFont.truetype('TakaoPGothic.ttf', 15)
# 拡大したい場合はsbの値を変更する
# ただし、値によっては、縮小されたり、拡大されたりして
# 見にくくなる。推奨はsb = 0.8もしくはz = 1
# sb = 0.8の場合は以下の2行をコメントアウトし、z = 1をコメントにする
# sb = 0.8
# z = sb * 40 / 15
z = 1
fn = 0
for i in range(max_count):
if xpos[i] == 0 and ypos[i] == 0:
break
if ypos[1] < 0:
locate_x = 25 * 8
locate_y = 1 * 16
if ypos[1] > 0:
locate_x = 25 * 8
locate_y = 22 * 16
sfmt = '%-8s での日食の模様' % (obs)
draw.text((locate_x, locate_y), sfmt, font=fonts)
if ypos[1] < 0:
locate_x = 15 * 8
locate_y = 2 * 16
if ypos[1] > 0:
locate_x = 15 * 8
locate_y = 23 * 16
sb = (sun_radius[i] + moon_radius[i] - math.sqrt(xpos[i] ** 2 + ypos[i] ** 2)) / (2.0 * sun_radius[i])
sfmt = '%4d 年 %2d 月 %2d 日 %2d 時 %2d 分 の欠け具合: 食分 = %5.2f' % (year[i], month[i], day[i], hour[i], minute[i], sb)
draw.text((locate_x, locate_y), sfmt, font=fonts)
# 太陽を描く
rr = int(sun_radius[1] * z + 0.5)
draw.ellipse(((80 - rr) * 4, (50 - rr) * 4, (80 + rr) * 4, (50 + rr) * 4), fill=sun_color)
# 月を描く
ll = int(moon_radius[i] * z + 0.5)
x = xpos[i] * z + 80
y = 50 - ypos[i] * z
x1 = x - ll
x2 = x + ll
y1 = y - ll
y2 = y + ll
# この判断分があると拡大したときに
# 日食が最後まで表示されないため、コメントにしている
# if x1 < 1 or x2 > 158:
# continue
# else:
# if y1 < 1 or y2 > 99:
# continue
draw.ellipse((x1 * 4, y1 * 4, x2 * 4, y2 * 4), fill=moon_color)
# ファイル番号を描画
drawing_file_number(fn, draw, fonts)
# 描画した日食の画像を保存
s = str(fn)
sfn = s.zfill(5)
img.save('./images/eclipse/eclipse' + sfn + '.png')
fn = fn + 1
# 画面クリア
draw.rectangle((1, 1, 639, 399), fill=(0, 0, 0))
# メイン
root = tk.Tk()
root.resizable(False, False)
root.geometry('642x440')
root.title('マイコン宇宙講座 - 日食シミュレーション・プログラム')
canvas = tk.Canvas(root, width=640, height=400, bg='black')
canvas.pack(anchor=tk.NW)
# 日食を描く
drawing_sun_eclipse()
# imagesフォルダ内にある画像ファイルを取得する
files = sorted(glob.glob('./images/eclipse/*.png'))
# カウンターとファイルの数を取得
file_number = len(files)
# 前の画像を表示
prev_button = tk.Button(root, text='Prev', width=6, relief=SOLID, cursor='hand1', command=display_eclipse_prev)
prev_button.place(x=8, y=409)
# 次の画像を表示
next_button = tk.Button(root, text='Next', width=6, relief=SOLID, cursor='hand1', command=display_eclipse_next)
next_button.place(x=86, y=409)
button = tk.Button(root, text='閉じる', width=6, relief=SOLID, cursor='hand1', command=root.destroy)
button.place(x=558, y=409)
# 最初の画像を表示
if file_number != 0:
count = 0
display_eclipse()
prev_button['state'] = tk.NORMAL
next_button['state'] = tk.NORMAL
else:
prev_button['state'] = tk.DISABLED
next_button['state'] = tk.DISABLED
root.mainloop()例題 1955年12月14日に起きた皆既日食の様子を見てみよう。場所は石垣島天文台、計算開始時刻は16時とします。
DATE AND TIME(JST) ? 19551214,160000
INTERVAL(UNIT OF MINUTE) ? 5
石垣島天文台 ( JST ) 月の座標 太陽と月の大きさ 食分
---------------------------------------------------------------------------------
年 月 日 時 分 - X - - Y - 。 。 ,
1955 12 14 16 30 33.1 -6.8 16.2 14.8 -0.09
12 14 16 35 31.2 -6.4 16.2 14.8 -0.03
12 14 16 40 29.3 -6.0 16.2 14.8 0.03
12 14 16 45 27.4 -5.5 16.2 14.8 0.09
12 14 16 50 25.5 -5.0 16.2 14.8 0.15
12 14 16 55 23.5 -4.6 16.2 14.8 0.22
12 14 17 0 21.6 -4.1 16.2 14.8 0.28
12 14 17 5 19.6 -3.6 16.2 14.8 0.34
12 14 17 10 17.6 -3.2 16.2 14.7 0.40
12 14 17 15 15.5 -2.7 16.2 14.7 0.47
12 14 17 20 13.5 -2.2 16.2 14.7 0.53
12 14 17 25 11.4 -1.7 16.2 14.7 0.60
12 14 17 30 9.3 -1.2 16.2 14.7 0.67
12 14 17 35 7.1 -0.8 16.2 14.7 0.73
12 14 17 40 5.0 -0.3 16.2 14.7 0.80
12 14 17 45 2.8 0.2 16.2 14.7 0.87
12 14 17 50 0.6 0.7 16.2 14.7 0.92
12 14 17 55 -1.6 1.2 16.2 14.7 0.89
12 14 18 0 -3.9 1.7 16.2 14.7 0.82
12 14 18 5 -6.1 2.2 16.2 14.7 0.75
12 14 18 10 -8.4 2.7 16.2 14.7 0.68
12 14 18 15 -10.8 3.2 16.2 14.7 0.61
12 14 18 20 -13.1 3.8 16.2 14.7 0.53
12 14 18 25 -15.5 4.3 16.2 14.7 0.46
12 14 18 30 -17.9 4.8 16.2 14.7 0.38
12 14 18 35 -20.3 5.3 16.2 14.7 0.31
12 14 18 40 -22.7 5.8 16.2 14.7 0.23
12 14 18 45 -25.2 6.3 16.2 14.7 0.15
12 14 18 50 -27.7 6.8 16.2 14.7 0.07
12 14 18 55 -30.2 7.3 16.2 14.7 -0.00
12 14 19 0 -32.7 7.9 16.2 14.7 -0.08
---------------------------------------------------------------------------------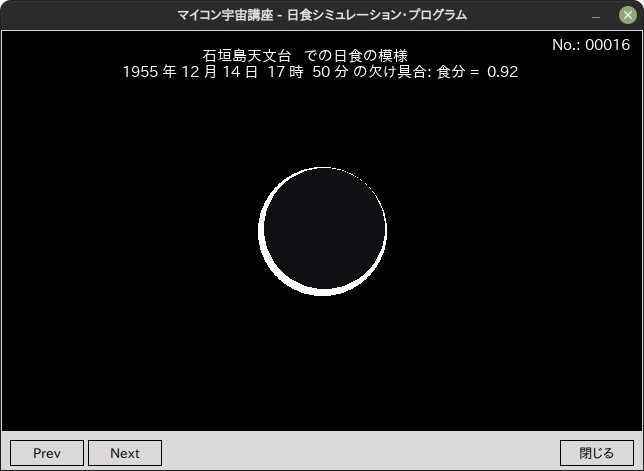
GIFアニメーション化してみました。表示されない場合はリロード(再読込み)を行ってください。

