マイコン宇宙講座-月食シミュレーション
月食は月が地球の影に入る現象のことです。この地球の影に入るということはどういうことでしょうか。月は地球の周りを公転しています。そのとき、月、地球、太陽というように一直線に並んだときに、太陽の光に照らされた地球には影ができます。その影に入ると、月食という現象が起きます。必ずしも毎回起きる現象ではありません。比較的レアな現象といってよいでしょう。ですから月食が起きると、ニュースになったりします。ただし、月食は起きるものの日本からは見えないこともあります。

月食には2つのパターンがあり、部分月食、皆既月食があります。部分月食は月が影の中に入ることはなく、部分的に入る現象のことです。それに対して皆既月食は、月が完全に影の中に入ってしまう現象です。面白いのは、月の99%が影の中に入ったとしても、残りの1%が入っていませんので部分月食となります。なかなかシビアですね。
日本で見ることができる2022年の月食は、11月8日の皆既月食のみです。それ以降も部分日食や皆既月食があります。国立天文台天文情報センター暦計算室のサイトに日月食データーベースがありますので確認してみるとよいでしょう。
サブルーチン sun
※サブルーチンはlib.pyに記述してください。
# SUN
def sun(ta, c, g, j, l, m, n, v):
# SUN-THETA
sx = - 1.000e-5 * ta * math.sin(g + l)
sx = sx - 1.000e-5 * math.cos(g - l - j)
sx = sx - 1.400e-5 * math.sin(2 * g - l)
sx = sx - 3.000e-5 * ta * math.sin(g - l)
sx = sx - 3.900e-5 * math.sin(n - l)
sx = sx - 4.000e-5 * math.cos(l)
sx = sx + 4.200e-5 * math.sin(2 * g + l)
sx = sx - 2.080e-4 * ta * math.sin(l)
sx = sx + 3.334e-3 * math.sin(g + l)
sx = sx + 9.999e-3 * math.sin(g - l)
sx = sx + 0.39793 * math.sin(l)
# SUN-RHO
sy = 2.7e-5 * math.sin(2 * g - 2 * v)
sy = sy - 3.3e-5 * math.sin(g - j)
sy = sy + 8.4e-5 * ta * math.cos(g)
sy = sy - 1.4e-4 * math.cos(2 * g)
sy = sy - 0.033503 * math.cos(g)
sy = sy + 1.000421
# SUN-PHI
sz = -1.700e-5 * math.cos(2 * g - 2 * v)
sz = sz - 1.900e-5 * math.sin(g - v)
sz = sz + 2.400e-5 * math.sin(4 * g - 8 * m + 3 * j)
sz = sz - 2.500e-5 * math.cos(g - j)
sz = sz + 3.000e-5 * math.sin(c - l)
sz = sz + 4.600e-5 * ta * math.sin(2 * l)
sz = sz + 6.801e-5 * math.sin(2 * g)
sz = sz - 7.900e-5 * math.sin(n)
sz = sz - 8.000e-5 * ta * math.sin(g)
sz = sz - 9.500e-5
sz = sz - 3.460e-4 * math.sin(g + 2 * l)
sz = sz - 1.038e-3 * math.sin(g - 2 * l)
sz = sz + 0.032116 * math.sin(g)
sz = sz - 0.041295 * math.sin(2 * l)
return sx, sy, szメインルーチン m59.py
# m59.py
# マイコン宇宙講座
# 5-9 月食シミュレーション・プログラム
from PIL import Image, ImageDraw, ImageFont
from tkinter.constants import SOLID
import tkinter as tk
import math
import lib
M2PI = 2.0 * math.pi
day = [0 for i in range(20)]
hour = [0 for i in range(20)]
minute = [0 for i in range(20)]
xpos = [0 for i in range(20)]
ypos = [0 for i in range(20)]
shadowsize = [0 for i in range(20)]
moonsize = [0 for i in range(20)]
print()
std = input('DATE AND TIME(JST) ? ')
dy, dt = std.split(',')
dy = float(dy)
dt = float(dt)
jd, yy, mm, dd, hh, ms, ss = lib.mjd(dy, dt)
iv = 30.0
i = 0
ii = 0
yz = 0
mz = 0
print()
print(' Date ( JST ) - X - - Y - 本影 月の大きさ')
print(' ---------------------------------------------------------------------------')
print(' 年 月 日 時 分 。 。 。 ,')
while True:
ta = (jd - 15019.5) / 36525.0
a, b, c, d, e, g, j, l, m, n, v, w = lib.argument(ta)
mx, my, mz = lib.moon(ta, a, b, d, e, n, g, w)
r0 = c
r1 = mx
r2 = my
r3 = mz
ra, dc, dl = lib.positions(r0, r1, r2, r3)
mr = ra
md = dc
rl = dl
sx, sy, sz = lib.sun(ta, c, g, j, l, m, n, v)
r0 = l
r1 = sx
r2 = sy
r3 = sz
ra, dc, dl = lib.positions(r0, r1, r2, r3)
ra += math.pi
dc = -(dc)
if ra > M2PI:
ra -= M2PI
# PRINT POSITIONS
x = -(mr - ra) * lib.K[3] * 60.0
y = (md - dc) * lib.K[3] * 60.0
rl = 6378.16 * rl
rr = 0.76 * math.atan(6378.16 / rl) * lib.K[3] * 60.0
ll = math.atan(1738.0 / rl) * lib.K[3] * 60.0
jd = jd + 0.375
yy, mm, dd = lib.jdate(jd, lib.T)
jd = jd - 0.375
hh = 24.0 * (dd - int(dd))
dd = int(dd)
ms = 60.0 * (hh - int(hh)) + 0.1
hh = int(hh)
if int(ms + 0.1) == 60:
hh = hh + 1
if hh == 24:
hh = 0
ms = 0
if (x ** 2 + y ** 2) > 16000.0 and (ii == 0):
jd += (iv / 1440.0)
continue
if (x ** 2 + y ** 2) > 16000.0:
break
else:
while True:
if int(ii / 2) != ii / 2:
break
i = i + 1
day[i] = dd
hour[i] = hh
minute[i] = ms
xpos[i] = x
ypos[i] = y
shadowsize[i] = rr
moonsize[i] = ll
break
sfmt = ' %2d %2d %2d %6.1f %6.1f %5.1f %5.1f' % (dd, hh, ms, x, y, rr, ll)
if yy != yz:
sfmt = ' %4d %2d %2d %2d %2d %6.1f %6.1f %5.1f %5.1f' % (yy, mm, dd, hh, ms, x, y, rr, ll)
else:
if mm != mz:
sfmt = ' %2d %2d %2d %2d %6.1f %6.1f %5.1f %5.1f' % (mm, dd, hh, ms, x, y, rr, ll)
print(sfmt)
yz = yy
mz = mm
ii += 1
if ii < 18:
jd += iv / 1440.0
continue
#break
print(' ---------------------------------------------------------------------------')
print()
std = input('PRESS ANY KEY')
# GESYOKU PLOT
root = tk.Tk()
root.resizable(False, False)
root.geometry('642x440')
root.title('マイコン宇宙講座 - 月食シミュレーションプログラム')
img = Image.new('RGB', (640, 400), (0, 0, 0))
draw = ImageDraw.Draw(img)
canvas = tk.Canvas(root, width=640, height=400, bg='black')
canvas.pack(anchor=tk.NW)
# Color
moon_color = (240, 210, 0)
shadow_color = (107, 2, 2)
# フォント名は実行環境に合わせて変更すること
# TrueTypeの等幅フォント名を指定する
fonts = ImageFont.truetype('TakaoPGothic.ttf', 15)
if ypos[1] < 0:
sfmt = '%4d 年 %2d 月 %2d 日の月食' % (yy, mm, day[1])
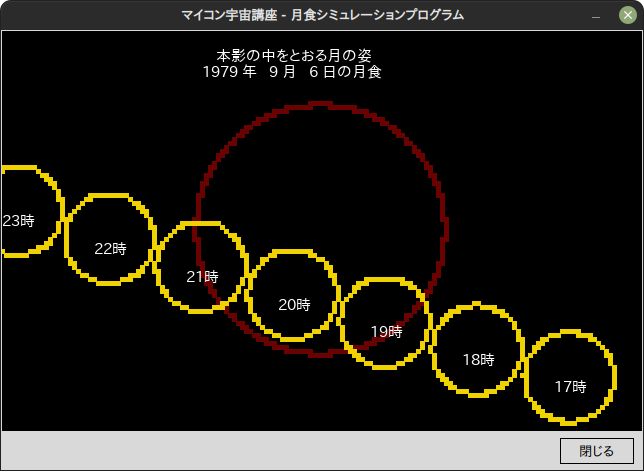
draw.text((214, 16), '本影の中をとおる月の姿', font=fonts)
draw.text((200, 32), sfmt, font=fonts)
else:
sfmt = '%4d 年 %2d 月 %2d 日の月食' % (yy, mm, day[1])
draw.text((214, 352), '本影の中をとおる月の姿', font=fonts)
draw.text((200, 368), sfmt, font=fonts)
rr = shadowsize[1]
for m in range(360):
x = rr * math.cos(m / lib.K[3]) / 1.5
y = rr * math.sin(m / lib.K[3]) / 1.5
x = int(80 + x) * 4
y = int(50 + y) * 4
draw.rectangle((x - 2, y - 2, x + 2, y + 2), fill=shadow_color)
for i in range(1, 10):
if xpos[i] == 0 and ypos[i] == 0:
break
xpos[i] = xpos[i] / 1.5 + 80
ypos[i] = 50 - ypos[i] / 1.5
x = xpos[i] / 2 - 2
y = ypos[i] / 4
if x < 0 or x > 75:
continue
if y < 0 or y > 24:
continue
sfmt = '%2d時' % (hour[i])
draw.text((x * 8, y * 16), sfmt, font=fonts)
if abs(minute[i]) > 1:
sfmt = '%2d分' % (minute[i])
draw.text((x * 8, y * 16 + 16), sfmt, font=fonts)
for m in range(0, 360, 4):
x = moonsize[i] * math.cos(m / lib.K[3]) / 1.5
y = moonsize[i] * math.sin(m / lib.K[3]) / 1.5
x = int(xpos[i] + x)
y = int(ypos[i] + y)
if x < 0 or x > 159:
continue
if y < 0 or y > 99:
continue
x = x * 4
y = y * 4
draw.rectangle((x - 2, y - 2, x + 2, y + 2), fill=moon_color)
# 描画した月食の画像を保存
img.save('./images/gesyoku.png')
# 月食表示
photo = tk.PhotoImage(file='./images/gesyoku.png')
canvas.create_image(1, 1, image=photo, anchor=tk.NW)
button = tk.Button(root, text='閉じる', width=6, relief=SOLID, cursor='hand1', command=root.destroy)
button.place(x=558, y=407)
root.mainloop()例題 1979年9月6日の月食を表示してみよう。時刻は17時とします。
DATE AND TIME(JST) ? 19790906,170000
Date ( JST ) - X - - Y - 本影 月の大きさ
---------------------------------------------------------------------------
年 月 日 時 分 。 。 。 ,
1979 9 6 17 0 93.2 -55.5 46.7 16.7
9 6 17 30 75.9 -50.3 46.7 16.7
9 6 18 0 58.7 -45.2 46.7 16.7
9 6 18 30 41.4 -40.0 46.7 16.7
9 6 19 0 24.1 -34.8 46.7 16.7
9 6 19 30 6.9 -29.6 46.7 16.7
9 6 20 0 -10.4 -24.4 46.7 16.7
9 6 20 30 -27.6 -19.2 46.7 16.7
9 6 21 0 -44.8 -14.0 46.6 16.7
9 6 21 30 -62.0 -8.7 46.6 16.7
9 6 22 0 -79.3 -3.5 46.6 16.7
9 6 22 30 -96.5 1.8 46.6 16.7
9 6 23 0 -113.7 7.1 46.6 16.7
---------------------------------------------------------------------------